Mosquito community diversity analysis with vegan
23 May 2017This tutorial is based on the data from this paper.
In this tutorial, I show how to use the R package vegan to analyze an original dataset on the abundance of mosquito species in the Raleigh-Durham area of North Carolina. I cover the calculation of common diversity indices, analysis of diversity measures with linear models, and visualization of patterns in community composition using multivariate ordination methods (constrained and unconstrained correspondence analysis).
Study design
We selected three regions in the Raleigh-Durham area (denoted DU, LW, and PR). Within each region, we identified three 200m transects that spanned a field-forest habitat gradient. We set up 5 traps along each transect, with the field-forest boundary located at the midpoint. Altogether, this resulted in 45 trap locations (3 regions x 3 transects x 5 trap locations).
Using 6-inch ground resolution imagery from the USGS Earth Explorer, we digitally classified the landscape within a 100 meter radius of each trap into 9 categories and computed the proportion of the landscape that fell into each category: grassland, deciduous tree canopy, evergreen tree canopy, mixed tree canopy, shrub, cultivated crops, barren land, pavement, and buildings.
To collect mosquitoes, CDC light traps were hung on T-shaped structures built from PVC pipes. Traps were baited with dry ice because host-seeking mosquitoes are drawn to carbon dioxide. Here is a schematic of our study design and a photo of our trap set-up:

Traps were set up at dusk and picked up at dawn. Mosquitoes were taken back to the lab and killed in a freezer before being identified to species level and counted. Collections took place once every 2 weeks over a 5 month period from June 1 to October 15, 2014.
The data
Open R and load vegan, installing it first if necessary:
# install package
install.packages("vegan")
# load package
library("vegan")
Import the data from GitHub and specify that Habitat is an ordered factor (this will be important for boxplots and linear models).
# read data from GitHub
data <- read.csv("https://raw.githubusercontent.com/rgriff23/Mosquito_ecology/master/Analysis/data.csv", row.names=1)
# make Habitat an ordered variable
data$Habitat <- ordered(data$Habitat, c("Field", "NearField", "Edge", "NearForest", "Forest"))
Take a few minutes to familiarize yourself with the data. There are 45 rows corresponding to 45 traps, and 36 columns which can be broken down as follows:
- columns 1-3: trap characteristics (region, transect, habitat)
- columns 4-8: landscape variables related to vegetation cover
- columns 9-12: landscape variables related to man-made structures
- column 13: number of trap-nights
- columns 14-36: abundance of mosquito species
I refer to these column numbers when subsetting the data below.
Does species diversity vary across habitats?
This first question requires us to compute mosquito species diversity indices for each trap location. We will compute three measures of species diversity:
- Richness, the total number of unique species found at a site
- Shannon-Weiner diversity, a common diversity index where species are weighted by abundance
- Rarefied richness, or species richness estimated with a resampling procedure to control for variation in sample size
Here is code to compute these metrics for each trap site:
# mosquito abundance matrix
abundance.matrix <- data[,14:36]
# store computed indices in a new data frame called 'indices'
indices <- data[,c("Region","Transect","Habitat")]
indices$Richness <- rowSums(abundance.matrix>0)
indices$Shannon <- diversity(abundance.matrix) # shannon is default
indices$Rarefied <- c(rarefy(abundance.matrix[1:45,], sample=15))
Use boxplots to visualize differences in species diversity along our field-forest habitat gradient:
par(mar=c(3,4,3,2), mfrow=c(2,2))
colors = terrain.colors(6)[5:1]
boxplot(Richness~Habitat, data=indices, boxwex=0.5, col=colors,
cex.axis=0.5, ylab="Richness")
boxplot(Shannon~Habitat, data=indices, boxwex=0.5, col=colors,
cex.axis=0.5, ylab="Shannon diversity")
boxplot(Rarefied~Habitat, data=indices, boxwex=0.5, col=colors,
cex.axis=0.5, ylab="Rarefied richness")
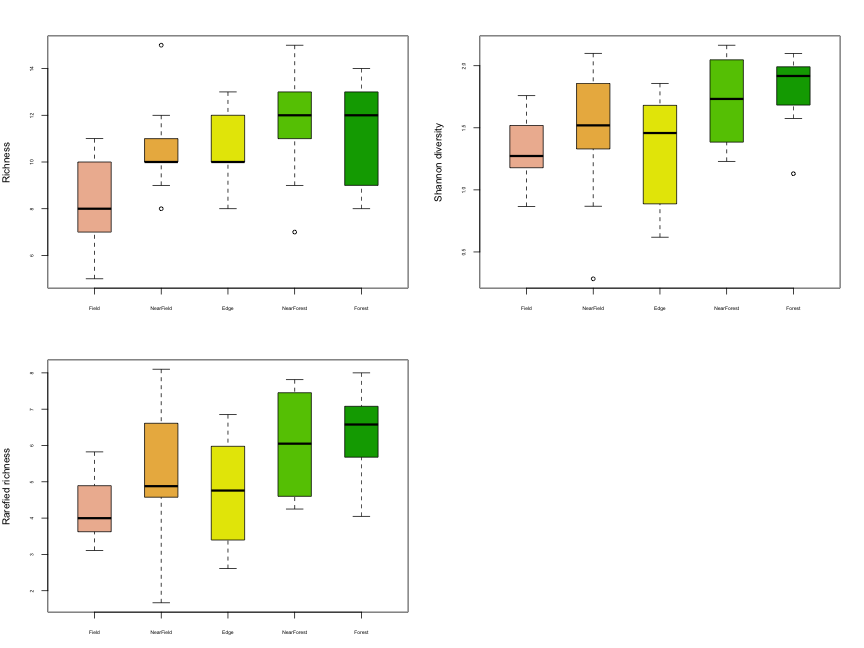
It appears that species diversity increases as we move from the field to the forest. We can test for differences among habitats statistically using a linear model, with Habitat as a predictor of species diversity:
# fit linear models
mod.richness <- lm(Richness~Habitat, data=indices)
mod.shannon <- lm(Shannon~Habitat, data=indices)
mod.rarefied <- lm(Rarefied~Habitat, data=indices)
# ANOVA
anova(mod.richness)
> Analysis of Variance Table
>
> Response: Richness
> Df Sum Sq Mean Sq F value Pr(>F)
> Habitat 4 57.2 14.30 2.9485 0.03164 *
> Residuals 40 194.0 4.85
> ---
> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
anova(mod.shannon)
> Analysis of Variance Table
>
> Response: Shannon
> Df Sum Sq Mean Sq F value Pr(>F)
> Habitat 4 1.7619 0.44048 2.395 0.06639 .
> Residuals 40 7.3565 0.18391
> ---
> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
anova(mod.rarefied)
> Analysis of Variance Table
>
> Response: Rarefied
> Df Sum Sq Mean Sq F value Pr(>F)
> Habitat 4 25.356 6.3389 2.8967 0.0339 *
> Residuals 40 87.533 2.1883
> ---
> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Species richness and rarefied richness are both significantly associated with habitat type (p < 0.05), while Shannon-Weiner diversity is close (p < 0.07). The estimated coefficients of the linear models tell us something about how species diversity is associated with habitat. Since Habitat is coded as an ordered variable (Field < NearField < Edge < NearForest < Forest), the output might look a little different than what you are used to for continuous or unordered categorical predictors. Look at the estimated coefficients for the richness model:
summary(mod.richness)
>
> Call:
> lm(formula = Richness ~ Habitat, data = indices)
>
> Residuals:
> Min 1Q Median 3Q Max
> -4.5556 -1.3333 -0.3333 1.6667 4.3333
>
> Coefficients:
> Estimate Std. Error t value Pr(>|t|)
> (Intercept) 10.4667 0.3283 31.882 <2e-16 ***
> Habitat.L 2.1082 0.7341 2.872 0.0065 **
> Habitat.Q -1.1284 0.7341 -1.537 0.1321
> Habitat.C 0.3514 0.7341 0.479 0.6348
> Habitat^4 -0.7171 0.7341 -0.977 0.3345
> ---
> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
>
> Residual standard error: 2.202 on 40 degrees of freedom
> Multiple R-squared: 0.2277, Adjusted R-squared: 0.1505
> F-statistic: 2.948 on 4 and 40 DF, p-value: 0.03164
There are four estimated coefficients: Habitat.L, Habitat.Q, Habitat.C, and Habitat^4. This is because ordered categories are modeled with a polynomial of order c - 1, where c is the number of levels in the category. In our case, our ordered category Habitat has 5 levels, so it will be modeled with a polynomial of order 5 - 1 = 4, e.g., y = a + bx + cx^2 + dx^3 + ex^4. In the model output, Habitat.L is the linear coefficient in the polynomial, b, Habitat.Q is the quadratic coefficient c, Habitat.C is the cubic coefficient d, and Habitat.^4 is of course e. Only the linear coefficient is significant in our models and the coefficient is positive, indicating that our mosquito diversity indices increase linearly as one moves from trap to trap along our field-forest transects.
Identifying major axes of variation in community composition
In this section we will perform some exploratory ordination analyses, which can help us identify 1) which collection sites are most similar in terms of their composition of mosquito species, 2) which mosquito species are most similar in terms of their distribution across collection sites, and 3) whether our environmental variables explain a significant amount of variation in mosquito communities. Ordination methods are generally used more for exploration and visualization than for hypothesis testing (although as I will demonstrate, hypothesis testing is possible with these models). Visualization is key though. A community diversity study like this would feel incomplete without some sort of ordination plot to visualize structure in our high dimensional data.
Ordination techniques fall into two major categories: unconstrained and constrained. Unconstrained methods (e.g., principal components and correspondence analysis) take a species abundance matrix and identify the axes that optimally account for variation in the data. Unconstrained methods are agnostic about what factors underly those axes of variation. In contrast, constrained ordination methods essentially combine unconstrained ordination with regression analysis, with the axes of variation being constrained to linear combinations of a set of predictor variables.
The vegan package provides functions for performing two popular families of ordination methods: cca for ‘correspondence analysis’, and rda for ‘redundancy analysis’. Which function you should use depends on your data. If you want differences in absolute abundance to matter then rda is better, but if you want to focus on relative abundances then cca is better. For example, if you have the following data:
> Sp.a Sp.b
> Site A 5 10
> Site B 50 100
If you want Sites A and B to be considered very similar because the proportions of species are the same, then you want cca, but if you want those sites to be considered very different because of the absolute abundances are quite different, then you want rda. Generally, if you have raw species abundance data then you will choose cca.
The following table summarizes how you can do both unconstrained and constrained ordination analyses using cca and rda:

Note that PCA is just an RDA without any explanatory variables, which is why you can run a PCA in vegan like this: rda(abundance.matrix).
In this tutorial, we will work through the three ordination methods on the bottom row of the table since we have raw species abundance data. First, we will apply correspondence analysis (CA) to the mosquito abundance matrix and visualize the major axes of variation in mosquito community composition. Next, we will perform a constrained CA, also known as canonical CA (CCA), bringing the environmental data into play as predictors of mosquito community composition. Finally, we will perform an extension of CCA called partial CCA (pCCA), in which predictor variables are separated into effects you are interested in (i.e., fixed effects) and effects you want to control for (i.e., random effects).
Before beginning, let’s make a couple of small adjustments to our abundance matrix. First, implement a square root transformation to dampen the influence of large counts on the results. Second, divide counts by the variable TrapNights to normalize for the variable number of trap nights due to trap failures.
abundance.matrix2 <- sqrt(abundance.matrix)/data$TrapNights
Correspondence analysis (CA)
For the CA, all we need is the abundance matrix.
# pca
my.ca <- cca(abundance.matrix2)
Let’s use a barplot to visualize how much of the variance is explained by each CA axes:
# barchart for variance of CA explained
barplot(my.ca$CA$eig/my.ca$tot.chi, names.arg = 1:my.ca$CA$rank, cex.names = 0.5, ylab="Proportion of variance explained", xlab="CA axis")
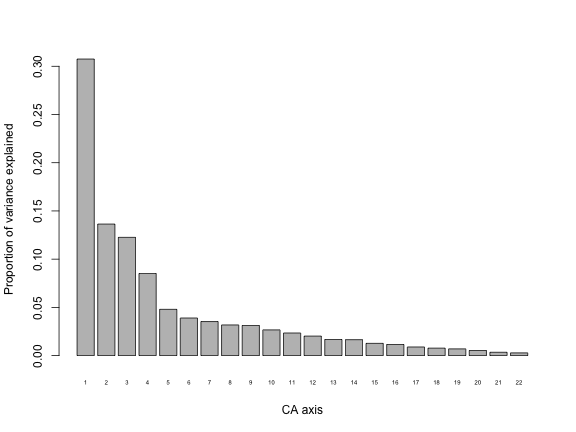
We can see that the first CA axis explains a little over 30% of variation in the data. Pull this information directly from the CA object like this:
# CA proportions of variance explained
head(my.ca$CA$eig/my.ca$CA$tot.chi)
> CA1 CA2 CA3 CA4 CA5 CA6
> 0.30749882 0.13638211 0.12259239 0.08522405 0.04795735 0.03898369
The fact that the first 2 axes only explain a combined ~44% of variation in the data indicates that mosquito community composition is not easily reduced to just one or two axes of variation. Let’s look at a scatterplot of our data with respect to the first two CAs:
# plot
plot(my.ca)
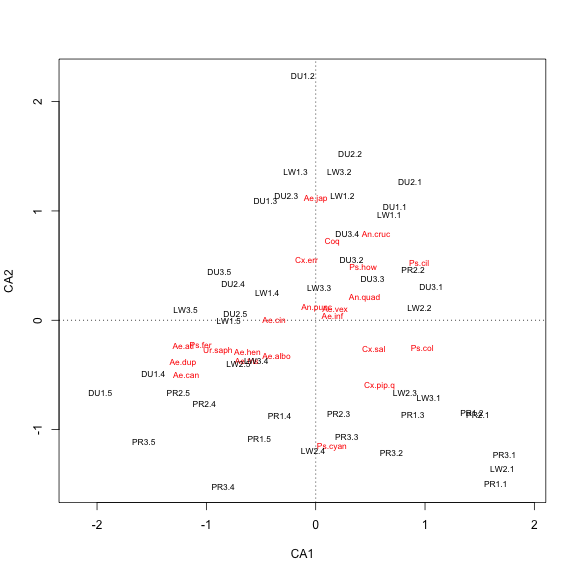
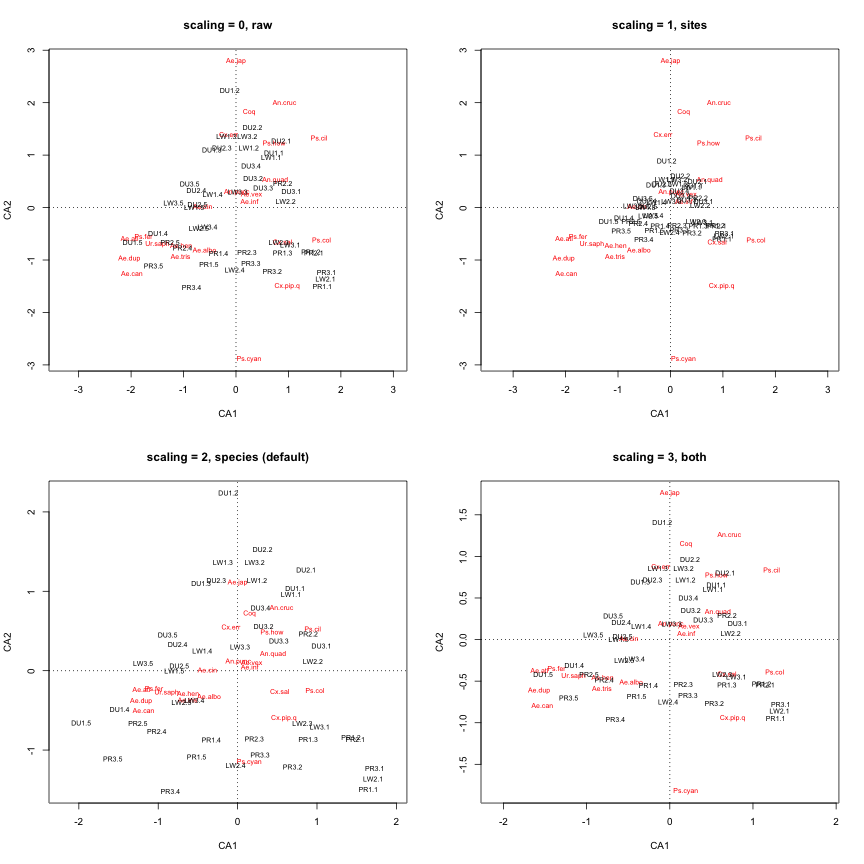
There are a few ways we can alter this plot to try to get a better picture of the data. One thing we can try is adjusting the scaling of the site and species scores in our plot. The plot.cca function (which is called when you use plot on a cca results) has an argument scaling that takes four values: 0 = no scaling, 1 = sites scores are scaled by eigenvalues, 2 = species scores are scaled by eigenvalues (the default), and 3 = both species and site scores are scaled by eigenvalues (alternatively, options 0-3 can be specified less cryptically with the character strings “none”, “sites”, “species”, and “symmetric”). Under option 1, site scores are weighted averages of species scores, and under option 2, species scores are weighted averages of site scores. Option 3 is a compromise between options 1 and 2, and is generally a good option for displaying sites and species in one plot.
Here is the effect these different options have on our plot:
# 4x4 PCA plots with different scaling options
layout(matrix(1:4,2,2,byrow=TRUE))
plot(my.ca, scaling="none", main="scaling = 0, raw")
plot(my.ca, scaling="sites", main="scaling = 1, sites")
plot(my.ca, scaling="species", main="scaling = 2, species (default)")
plot(my.ca, scaling="symmetric", main="scaling = 3, both")
An alternative way to make more space on our plot is to simply display the sites and species on separate plots. Let’s also add colors to our site labels to represent different habitats, and increase the size of the labels.
# 2 panels
layout(matrix(1:2,1,2))
# plot sites
site.cols <- rep(terrain.colors(6)[5:1],9)
plot(my.ca, display="sites", type="n", main="Sites", scaling="sites")
text(my.ca, display="sites", col=site.cols, scaling="sites")
# plot species
plot(my.ca, display="species", type="n", ylab="", main="Species", scaling="species")
text(my.ca, display="species", col="black", scaling="species")
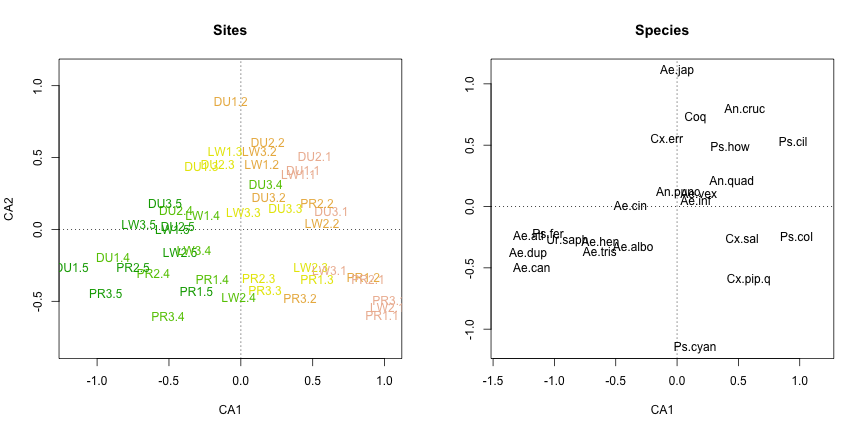
That’s better. The color coding helps reveal that the first CA axis reflects a forest-field gradient, suggesting that this habitat gradient is the most important factor structuring mosquito community composition. It also seems like there might be some differentiation among regions, with DU sites clustering near the top of the graph and PR/LW clustering near the bottom.
With the sites and species separated out, it is easier to see the differentiation among species as well. Given that CA1 appears to be a forest-field gradient, we can see that some mosquito species tend to be found in the forest (e.g. Ae.can and Ae.dup), while others tend to be found in the field (e.g. Ps.col and Ps.cil). And if we are correct that CA2 corresponds to a regional axis, then Ae.jap appears to have an affinity for the DU region (but not much preference for field or forest), while Ps.cyan has an affinity for the PR/LW regions (and similarly little preference for field or forest). Species near the center of the graph do not show much differentiation among either regions or habitats.
Canonincal correspondence analysis (CCA)
Now we will bring in the landscape variables. Let’s make a subset of the data for the landscape variables related to vegetation cover- these will be our predictor variables:
# predictor variables
fixed <- data[,4:8]
Run the CCA and compute variance inflation factors (VIF) to check for redundancy in the predictor variables. As a rule of thumb, VIF > 10 indicates problematic levels of redundancy. Redundant predictor variables do not adversely effect model fit, but it does make it difficult to interpret the estimated effects of individual predictor variables.
# the formula notation y ~ . means that all variables in 'fixed' should be included
my.cca <- cca(abundance.matrix2 ~ ., data=fixed)
# VIFs
vif.cca(my.cca)
> DeciduousForest EvergreenForest Grassland MixedForest
> 10.531727 8.810276 16.136888 5.159791
> ShrubScrub
> 1.173755
It seems we have some problematic redundancy in our predictor variables. A principled way to choose which variable(s) to drop is to use the drop1 function, which compares the change in AIC the results from dropping each variable from the full model:
drop1(my.cca, test="perm")
> Df AIC F Pr(>F)
> <none> 41.478
> DeciduousForest 1 42.643 2.8418 0.045 *
> EvergreenForest 1 43.179 3.3425 0.025 *
> Grassland 1 42.769 2.9589 0.040 *
> MixedForest 1 41.828 2.0902 0.100 .
> ShrubScrub 1 42.283 2.5082 0.080 .
> ---
> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
It looks like dropping MixedForest would have the least negative effect on the AIC. Let’s try dropping it and refitting the CCA:
# drop MixedForest from the fixed effects
fixed <- fixed[,-4]
# rerun the cca
my.cca <- cca(abundance.matrix2 ~ ., data=fixed)
# VIFs
vif.cca(my.cca)
> DeciduousForest EvergreenForest Grassland ShrubScrub
> 2.458115 4.038419 4.528197 1.094313
It seems like that did the trick- all of our VIFs are now reasonable. Let’s visualize the proportion of variance explained by each CCA axis with a barplot:
barplot(my.cca$CA$eig/my.cca$tot.chi, names.arg = 1:my.cca$CA$rank, cex.names = 0.5, ylab="Proportion of variance explained", xlab="CCA axis")
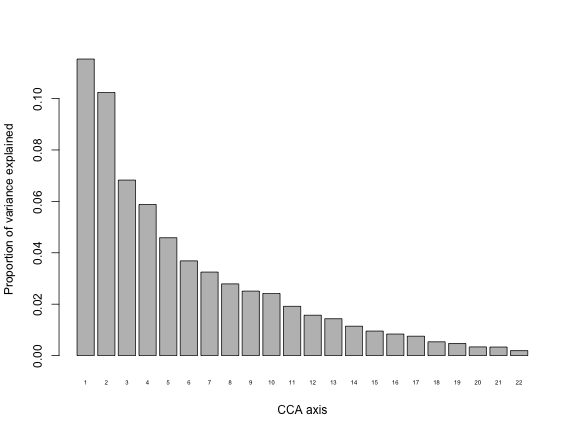
The first axis explains over 10% of the variance. Contrast this with the CA, for which the first axis explained ~31% of the variation in the data. It is expected that the CCA axes will explain less variation than the CA axes because they are now constrained to be linear combinations of the predictors, whereas CA did not have any constraints.
Look at CCA plots:
# 2 panels
layout(matrix(1:2,1,2))
# plot sites
plot(my.cca, display=c("sites", "bp"), type="n", main="Sites", scaling="sites")
text(my.cca, display="sites", col=site.cols, scaling="sites")
text(my.cca, display="bp", col="red")
# plot species
plot(my.cca, display=c("species", "bp"), type="n", ylab="", main="Species", scaling="species")
text(my.cca, display="species", col="black", scaling="species")
text(my.cca, display="bp", col="red")
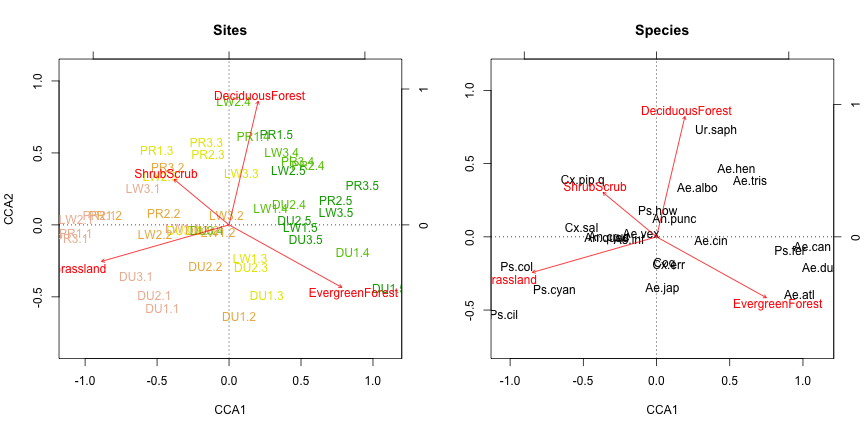
As in the CA, we can see the field-forest gradient reflected along the first axis of variation (note that the direction of the gradient is arbitrary).
Now extract the percent of variance explained by our predictor variables and test for a significant effect of our predictor variables on mosquito community composition:
# proportion of variance explained
my.cca$CCA$tot.chi/my.cca$tot.chi
> [1] 0.3580097
# significance test for individual predictors (type 3 test)
anova(my.cca, by="margin")
> Permutation test for cca under reduced model
> Marginal effects of terms
> Permutation: free
> Number of permutations: 999
>
> Model: cca(formula = abundance.matrix2 ~ DeciduousForest + EvergreenForest + Grassland + ShrubScrub, data = fixed)
> Df ChiSquare F Pr(>F)
> DeciduousForest 1 0.03706 1.9912 0.108
> EvergreenForest 1 0.04684 2.5172 0.064 .
> Grassland 1 0.06610 3.5516 0.021 *
> ShrubScrub 1 0.04907 2.6369 0.045 *
> Residual 40 0.74440
> ---
> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# significance test for entire model
anova(my.cca)
> Permutation test for cca under reduced model
> Permutation: free
> Number of permutations: 999
>
> Model: cca(formula = abundance.matrix2 ~ DeciduousForest + EvergreenForest + Grassland + ShrubScrub, data = fixed)
> Df ChiSquare F Pr(>F)
> Model 4 0.41512 5.5766 0.001 ***
> Residual 40 0.74440
> ---
> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
The vegetation cover variables explain about 36% of variance in mosquito community composition, and the strongest predictor variable is Grassland. The full model is statistically significant (p < 0.001).
Partial canonincal correspondence analysis (pCCA)
For our final ordination example, we will build on our CCA by incorporating a second matrix of landscape variables related to man-made structures as a ‘random effect’. This matrix is called the ‘conditioning matrix’ in the vegan documentation. The effects of these variables will be partialled out of the abundance matrix prior to estimating the effects of the ‘fixed effects’, which in our case are the landscape variables related to vegetation that we used in the CCA. Let’s make a subset of the data for the random effects:
# random effects
random <- data[,9:12]
Run the pCCA and check the VIFs:
# pcca
my.pcca <- cca(X=abundance.matrix2, Y=fixed, Z=random)
# VIFs
vif.cca(my.pcca)
> BarrenLand Building Pavement CultivatedCrops
> 2.874614 2.931234 1.144108 1.200515
> DeciduousForest EvergreenForest Grassland ShrubScrub
> 2.841406 4.717601 4.883144 1.223347
The VIFs are acceptable. Make the figures for the pCCA:
# 2 panels
layout(matrix(1:2,1,2))
# plot sites
plot(my.pcca, display=c("sites", "bp"), type="n", main="Sites", scaling="sites")
text(my.pcca, display="sites", col=site.cols, scaling="sites")
text(my.pcca, display="bp", col="red")
# plot species
plot(my.pcca, display=c("species", "bp"), type="n", ylab="", main="Species", scaling="species")
text(my.pcca, display="species", col="black", scaling="species")
text(my.pcca, display="bp", col="red")
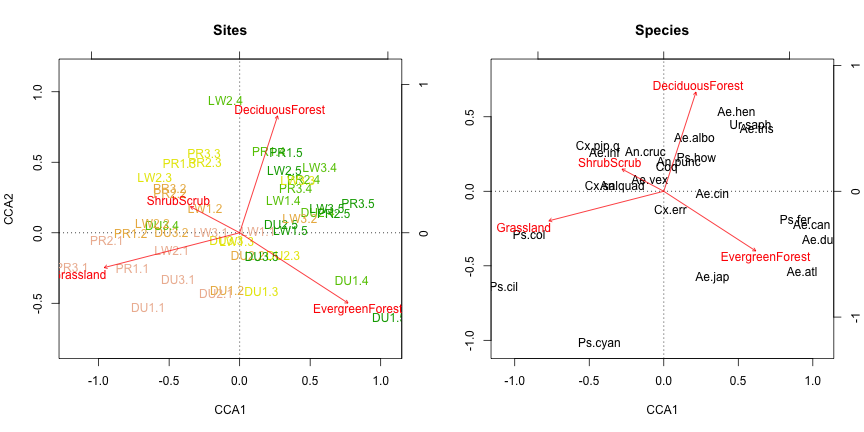
Not a whole lot has changed compared to the CCA. Compute the percent of variation explained by the predictors and test for signficance:
# proportion of variance explained
my.pcca$CCA$tot.chi/my.pcca$tot.chi
> [1] 0.319155
# significance test
anova(my.pcca)
> Permutation test for cca under reduced model
> Permutation: free
> Number of permutations: 999
>
> Model: cca(X = abundance.matrix2, Y = fixed, Z = random)
> Df ChiSquare F Pr(>F)
> Model 4 0.37007 5.2428 0.001 ***
> Residual 36 0.63527
> ---
> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Recall that in our CCA, the predictors explained 36% of variation. Since the pCCA random effects account for some additional variation in the data, the predictor variables explain a slightly smaller overall proportion, about 32%.
Concluding remarks
Our analyses showed that both mosquito community diversity and mosquito community composition vary along a field-forest gradient, with the forest having greater diversity than the field. Our visualizations allowed us to identify mosquito species that strongly prefer either the forest (e.g., Ae.can and Ae.dup) or the field (e.g., Ps.cil and Ps.col). The fact that the leading axes of the CA and CCA ordinations both represent a field-forest gradient suggests that the vegetation variables being included in the CCA represent the dominant axis of variation in the abundance data.
One of the most confusing things about ordination is figuring out how the different methods relate to one another and which one to use. The good news is that all of these methods tend to produce comparable results for a given dataset. Choosing the best one for your data is largely an art. You can try running both rda and cca to see which approach yields better visualizations of your data, and try different ways of scaling the scores (see the?plot.cca help page and the vegan design decisions document to read more about scaling options). The goal is simply to get a birds-eye view of the major patterns across your dataset in as clear a way as possible.
Footnotes:
For more information on species diversity indices, the vegan documentation is great and will point you toward any more specific literature you might want to look at. Try ?diversity and ?rarefy.
For more information on ordination methods, the vegan package provides a simple introduction in this vignette, and the package author provides a more thorough introduction in this tutorial. A good tutorial for customizing the appearance of vegan ordination plots can be found here
